
When it comes to exploring the intricate wonders of the mathematical world, one cannot ignore the captivating allure of Galexe Polyhedra. These intricate geometric shapes, named after the renowned mathematician Axel Galfre, offer a mesmerizing glimpse into the elegant beauty of mathematics.
At their core, Galexe Polyhedra are three-dimensional structures composed of polygons, making them a fascinating subject of study for mathematicians, scientists, and artists alike. Their symmetrical patterns and intricate details have captivated minds for centuries, offering endless possibilities for exploration and discovery.
What sets Galexe Polyhedra apart from other geometric shapes is their inherent complexity and versatility. Each Galexe Polyhedron is unique, consisting of multiple polygons carefully arranged to create an intricate framework. The interplay of lines and angles creates a visually stunning spectacle, revealing the intrinsic beauty hidden within the realm of mathematics.
Furthermore, the study of Galexe Polyhedra extends beyond their visual appeal, delving into the mathematical principles that govern their formation. The exploration of their properties reveals a fascinating interplay between symmetry, proportion, and spatial relationships. From the Fibonacci sequence to the golden ratio, Galexe Polyhedra unveils the underlying mathematical principles that govern the world around us.
This article will serve as a gateway to this captivating world, shedding light on the intricate wonders of Galexe Polyhedra. Join us on this journey of discovery as we unlock the secrets hidden within their mesmerizing structures. Prepare to be amazed by the mathematical beauty that awaits!
The History and Origins of Galxe Polyhedra
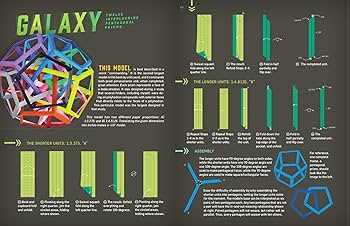
Galxe polyhedra, a fascinating class of geometric shapes, have a rich history rooted in ancient mathematical discoveries. The origins of Galxe polyhedra can be traced back to the works of ancient Greek mathematicians such as Euclid and Archimedes, who laid the foundation for the study of polyhedra.
Euclid, known as the “Father of Geometry,” wrote the influential mathematical treatise called Elements, which presented a comprehensive study of geometry. In Elements, Euclid described various polyhedra, including the five Platonic solids – the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. These solids served as the basis for further exploration of polyhedra by future mathematicians.
Archimedes, another renowned Greek mathematician, also made significant contributions to the field of polyhedra. In his work On the Sphere and Cylinder, Archimedes described the process of truncating a regular octahedron to obtain a shape that later became known as the truncated octahedron, one of the Archimedean solids.
The study of polyhedra continued to evolve over the centuries, with mathematicians like Kepler and Euler making important discoveries. Johannes Kepler was particularly fascinated by the relationship between the Platonic and Archimedean solids and their geometric properties. His work paved the way for further exploration of polyhedra and laid the groundwork for the development of Galxe polyhedra.
The term “Galxe polyhedra” itself was coined in modern times to describe a family of polyhedra that possess unique properties. These polyhedra are formed by truncating certain vertices of the Archimedean solids, resulting in intricate and aesthetically pleasing geometric shapes.
Today, Galxe polyhedra continue to captivate mathematicians and researchers, who explore their mathematical beauty and uncover new properties and applications. The study of Galxe polyhedra plays a crucial role in various fields, including architecture, crystallography, and materials science.
As we delve deeper into the fascinating world of Galxe polyhedra, we can appreciate the historical journey that has led to the discovery and exploration of these remarkable geometric shapes.
Exploring the Ancient Origins and Development
Polyhedra, three-dimensional figures with flat faces and straight edges, have been a subject of fascination and study for centuries. The origins of polyhedra can be traced back to ancient civilizations, where they were used for various purposes, including decoration, architecture, and even religious rituals.
The ancient Egyptians, for example, used polyhedra in their architectural designs, such as the pyramids. These structures were not only a symbol of the pharaoh’s power but also a testament to the Egyptians’ understanding of geometry and mathematics. The pyramids, with their triangular faces and square bases, are examples of polyhedra known as pyramids.
Ancient Greek mathematicians were also intrigued by polyhedra and made significant contributions to the field. The mathematician Euclid, known for his work in geometry, described and classified several types of polyhedra in his book “Elements.” His classification system laid the foundation for the study of polyhedra for centuries to come.
During the Renaissance, polyhedra gained widespread attention as artists, architects, and mathematicians explored their aesthetic and mathematical properties. The Italian mathematician Leonardo da Vinci, known for his art and inventions, was particularly fascinated by polyhedra and incorporated them into his work. His famous drawing, “The Study of Polyhedra,” showcases his exploration of these geometric figures.
In the modern era, polyhedra continue to be an area of study and fascination for mathematicians and scientists. Their properties and symmetries have applications in various fields, such as crystallography, physics, and computer graphics. The study of polyhedra has also expanded to include more complex and abstract forms, such as non-convex polyhedra and higher-dimensional polytopes.
|
|
Today, mathematicians and researchers continue to unlock the secrets of polyhedra, revealing their mathematical beauty and significance. Through the use of advanced mathematical tools and computer simulations, they are able to explore the vast universe of polyhedra, uncovering new discoveries and applications. |
Overall, the ancient origins and development of polyhedra have shaped our understanding of geometry and mathematics. From ancient civilizations to modern research, the study of polyhedra has played a crucial role in unlocking the fascinating world of mathematical beauty.
Uncovering the Mathematical Principles

The fascinating world of Galaxy Polyhedra is full of mathematical principles waiting to be uncovered. When exploring the intricate structures of these polyhedra, it becomes clear that they are not simply random shapes, but instead follow specific mathematical rules and principles.
The Golden Ratio
One of the most prominent mathematical principles found in Galaxy Polyhedra is the Golden Ratio. This ratio, approximately equal to 1.618, can be seen in the proportions and dimensions of various elements within the polyhedra.
For example, the relationship between the length of the edges and the dimensions of the faces often exhibit the Golden Ratio. This creates a sense of harmony and balance in the overall structure of the polyhedra, appealing to our aesthetic senses.
The Platonic Solids

Another mathematical principle that can be uncovered in Galaxy Polyhedra is the concept of the Platonic Solids. These are regular, convex polyhedra in which all faces are congruent and all vertices are identical.
In the realm of Galaxy Polyhedra, the Platonic Solids play a significant role in the formation of the polyhedra. The relationships between the number of faces, edges, and vertices in these solids help determine the overall structure and symmetry of the polyhedra.
Understanding the mathematical principles behind Galaxy Polyhedra allows us to appreciate the intricate beauty and elegance of these structures. It also provides a deeper insight into the underlying mathematical framework of the universe.
Applications of Galxe Polyhedra in Various Fields

Galxe polyhedra, with their fascinating mathematical properties, have found applications in a wide range of fields. Here are some examples:
Architecture: Galxe polyhedra are admired for their intricate and symmetrical structures. Architects have used these polyhedra as inspiration for designing unique and visually appealing buildings, bridges, and other structures.
Engineering: The geometric properties of Galxe polyhedra make them useful in engineering applications. These polyhedra can be used to optimize the strength and stability of structures, enhance fluid flow in pipelines, and design efficient mechanisms.
Chemistry: Galxe polyhedra have also found applications in chemistry. They can be used as molecular frameworks for organizing and stabilizing clusters of atoms or molecules, enhancing catalytic reactions, and creating new materials with specific properties.
Computer Science: Galxe polyhedra have been used in computer graphics and animation to create complex shapes and models. Their mathematical properties make them suitable for generating visually appealing and realistic 3D objects.
Art and Design: Artists and designers often draw inspiration from Galxe polyhedra to create aesthetically pleasing patterns, sculptures, and jewelry. The intricate and symmetrical nature of these polyhedra adds a unique touch to various art forms.
Mathematics Education: Galxe polyhedra can be used as teaching tools to introduce basic and advanced mathematical concepts to students. They help make geometry more engaging and provide a tangible representation of abstract mathematical principles.
In conclusion, the applications of Galxe polyhedra are diverse and extend across various fields. Their geometric properties and mathematical beauty make them useful in architecture, engineering, chemistry, computer science, art, design, and mathematics education.
Architecture and Design

Architecture and design have long been influenced by the captivating world of galxe polyhedra. The intricate geometric structures of polyhedra have served as inspiration for architects and designers, who have incorporated these fascinating shapes into their creations.
Utilizing Geometric Forms

Architects have often used polyhedra as a basis for creating buildings and structures. The symmetrical nature of polyhedra and their ability to be transformed into different forms make them ideal for inspiring unique architectural designs. By utilizing geometric forms found in galxe polyhedra, architects have been able to create visually striking and innovative structures.
For example, a building inspired by a dodecahedron – a polyhedron with twelve pentagonal faces – might feature a façade composed of pentagonal windows or a roof with a pentagonal shape. This incorporation of polyhedra into architecture adds a sense of mathematical beauty to the design, while also providing structural stability and strength.
Aesthetic Appeal

The aesthetic appeal of galxe polyhedra extends beyond architecture into the realm of design. Furniture designers, for instance, have drawn inspiration from the intricate patterns and shapes of polyhedra to create unique and visually stunning pieces.
The precise angles and symmetrical lines of polyhedra can be seen in the design of chairs, tables, and even lighting fixtures. By incorporating the geometric forms of polyhedra, furniture designers can create pieces that are not only functional but also act as works of art, adding an element of mathematical elegance to any space.
Conclusion: The world of galxe polyhedra has a profound impact on the fields of architecture and design. From inspiring innovative architectural structures to influencing the aesthetic appeal of furniture designs, polyhedra bring a sense of mathematical beauty to these fields. By unlocking the fascinating world of polyhedra, architects and designers continue to create captivating works that marry artistry and mathematical precision in extraordinary ways.
Chemistry and Material Science

Chemistry and material science play a crucial role in the study of galxe polyhedra. Galxe polyhedra are solid structures composed of interconnected galex molecules. Galex molecules are unique because of their ability to bond in a way that forms intricate and symmetrical patterns.
Chemists and material scientists are interested in galxe polyhedra because of their potential applications in various fields. Understanding the chemistry behind the formation and stability of these polyhedra can provide insights into designing new materials with specific properties.
One area where galxe polyhedra are being explored is in the development of advanced catalysts. Catalysts are substances that speed up chemical reactions without being consumed in the process. Galxe polyhedra with specific shapes and sizes can act as effective catalysts for certain reactions, enabling faster and more efficient synthesis of important molecules.
In addition, the unique properties of galxe polyhedra make them suitable for applications in nanotechnology. Nanotechnology involves manipulating matter at the atomic and molecular scale to create new materials with enhanced properties. Galxe polyhedra can be used as building blocks for constructing nanoscale structures with precise control over shape and composition.
Furthermore, the study of galxe polyhedra can contribute to the field of crystallography. Crystallography is the branch of science that studies the structure and properties of crystals. Galxe polyhedra exhibit crystal-like characteristics, and their study can provide valuable insights into crystal growth and the arrangement of atoms in solid materials.
Overall, the fields of chemistry and material science play a vital role in unlocking the potential of galxe polyhedrа. Through a deep understanding of their chemistry and properties, scientists can harness the mathematical beauty of galxe polyhedra for a wide range of applications in various industries.
Question-answer:
What are galxe polyhedra?
Galxe polyhedra are complex three-dimensional geometric shapes that have unique mathematical properties and symmetry. They are formed by combining regular polyhedra and transforming them in specific ways.
How are galxe polyhedra different from regular polyhedra?
Galxe polyhedra are different from regular polyhedra because they have additional faces and edges created through a process called “edgification”. This process adds new symmetry and complexity to the shapes, making them fascinating objects to study mathematically.
What are some examples of galxe polyhedra?
Some examples of galxe polyhedra include the Stella octangula, the great rhombicuboctahedron, and the deltoidal icositetrahedron. These shapes have intricate patterns and symmetries that make them visually appealing and mathematically interesting.
What practical applications do galxe polyhedra have?
While galxe polyhedra do not have direct practical applications, they are important for the study of mathematical symmetry and geometry. Understanding the properties of these complex shapes can help us develop new algorithms, solve geometric problems, and explore the limits of mathematical knowledge.



