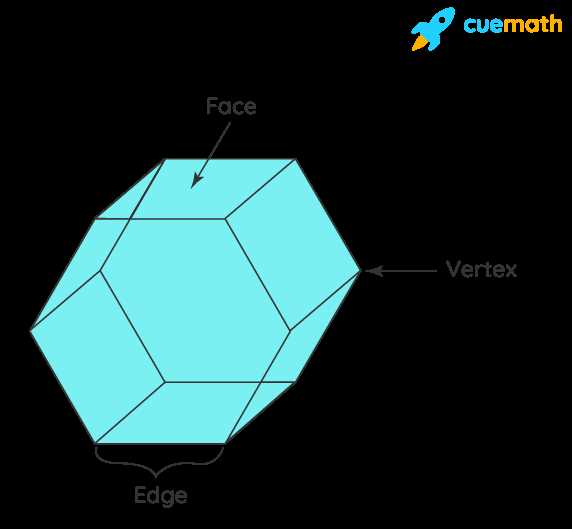
The study of polyhedra has long fascinated mathematicians and puzzle enthusiasts alike. One type of polyhedra that has gained significant attention is the Galxe polyhedra. These intricate three-dimensional structures have a unique and mesmerizing appearance, making them visually appealing and intellectually stimulating. Moreover, Galxe polyhedra have been found to have a deep connection with various mathematical puzzles, leading to exciting discoveries and challenges for problem solvers.
Galxe polyhedra, named after the mathematician who first described them, are defined as polyhedra with regular faces and equivalent vertices. This means that all the faces of a Galxe polyhedron are identical, and each vertex is surrounded by the same number of edges. These properties give rise to symmetrical and aesthetically pleasing shapes, which have been a subject of fascination for artists, architects, and mathematicians throughout history.
Mathematical puzzles involving Galxe polyhedra often revolve around their unique properties and transformations. For example, one common puzzle is to determine the number of possible rotations and reflections of a specific Galxe polyhedron. This requires a deep understanding of the symmetries and transformational symmetries of the polyhedron, making it a challenging exercise in spatial reasoning and abstract thinking.
Another popular puzzle involving Galxe polyhedra is the construction of larger structures using smaller ones. By combining multiple Galxe polyhedra in specific ways, mathematicians and puzzle enthusiasts have managed to create stunning and complex structures that defy intuition. These constructions often involve clever manipulation of the polyhedra’s symmetrical properties, leading to beautiful and unexpected results.
In conclusion, the study of Galxe polyhedra offers a fascinating journey into the world of mathematical puzzles. These intricately designed three-dimensional structures not only captivate the eye but also challenge the mind. By exploring their unique properties and transformations, mathematicians and puzzle enthusiasts can unlock a world of mathematical beauty and intellectual stimulation. So, if you find yourself captivated by the allure of Galxe polyhedra, don’t hesitate to dive into the world of mathematical puzzles and discover the limitless possibilities that lie within.
The Fascinating Relationship
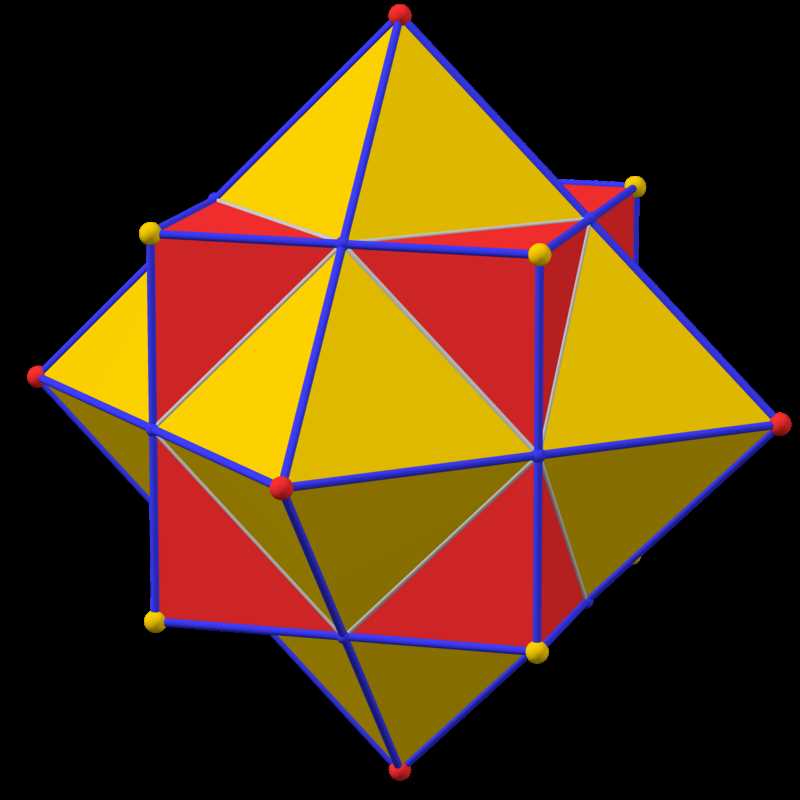
The relationship between Galxe polyhedra and mathematical puzzles is a truly fascinating one. These geometric shapes not only provide an aesthetic appeal, but they also serve as the foundation for a wide range of mathematical challenges.
When exploring the world of mathematical puzzles, one cannot help but encounter the intricate connections between these puzzles and Galxe polyhedra. These polyhedra, with their unique geometry and symmetrical patterns, lend themselves perfectly to the creation of mind-bending riddles.
Take, for example, the famous puzzle known as the “Soma cube.” This puzzle consists of seven irregularly shaped pieces that can be assembled to form a cube. The challenge lies in finding all the possible ways to arrange these pieces to create the cube. Interestingly, the shapes of these puzzle pieces correspond to the different faces of a Galxe polyhedron, further emphasizing the close relationship between these two concepts.
Another intriguing puzzle that showcases the connection between Galxe polyhedra and mathematical challenges is the “Tower of Hanoi.” In this puzzle, a set of disks of different sizes are stacked on one peg, with the objective being to transfer all the disks to another peg, using a third peg as an intermediate. The number of possible moves required to solve the puzzle follows a distinct pattern that can be visualized using a Galxe polyhedron.
Furthermore, the concept of symmetry, which is inherent in Galxe polyhedra, plays a significant role in many types of mathematical puzzles. For instance, puzzles involving rotational symmetry often rely on the properties of Galxe polyhedra to create visually pleasing and intellectually stimulating challenges.
In conclusion, the relationship between Galxe polyhedra and mathematical puzzles is a captivating one. These geometric shapes provide the foundation for a multitude of intriguing challenges, showcasing their versatility and beauty. Exploring this fascinating relationship not only deepens our understanding of both Galxe polyhedra and mathematical puzzles, but it also highlights the interconnectedness of different branches of mathematics.
Exploring the Intricacies

When delving into the world of galxe polyhedra and mathematical puzzles, it becomes apparent that there are countless intricacies to uncover. From the complex calculations involved in determining the various properties of these polyhedra to the creative problem-solving required to solve the puzzles they often represent, exploring this topic is a journey that is both stimulating and rewarding.
One of the most fascinating aspects of galxe polyhedra is the symmetry they exhibit. Not only do these polyhedra possess rotational symmetry, but they also possess reflectional symmetry. This means that they can be rotated or reflected in such a way that they appear identical from multiple perspectives. Understanding and manipulating these symmetries is essential for both analyzing and constructing galxe polyhedra.
Another intriguing feature of galxe polyhedra is their connection to mathematical puzzles. Many mathematical puzzles can be represented using these polyhedra, with the solutions often requiring a deep understanding of their properties. For example, the famous Rubik’s Cube is a three-dimensional galxe polyhedra puzzle that has captivated millions of people worldwide. Solving this puzzle requires a combination of logical thinking, pattern recognition, and spatial reasoning.
Exploring the intricacies of galxe polyhedra and mathematical puzzles also provides valuable insights into other mathematical concepts. For instance, the study of polyhedral graphs, which are graphs that represent the edges and vertices of polyhedra, has applications in network theory and optimization algorithms. Additionally, the study of recreational mathematics, which often involves solving mathematical puzzles for pure enjoyment, can contribute to the development of problem-solving skills and mathematical creativity.
In conclusion, delving into the intricacies of galxe polyhedra and mathematical puzzles opens up a world of fascinating discoveries. From the symmetries inherent in these polyhedra to the problem-solving skills required to tackle the puzzles they represent, exploring this topic offers a rich and rewarding experience for mathematicians and puzzle enthusiasts alike.
Unraveling the Secrets
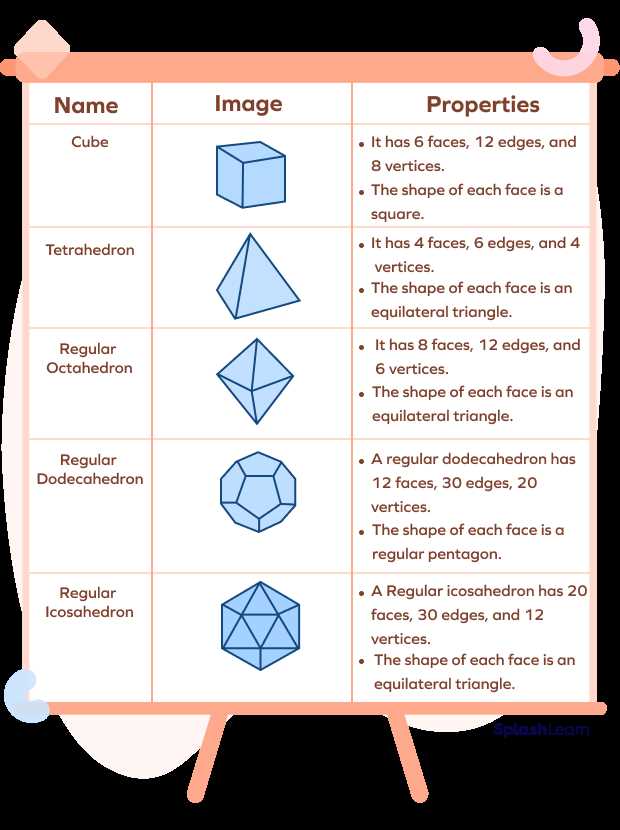
Galaxy Polyhedra, also known as astrohedra, have long been a fascination for mathematicians and puzzle enthusiasts alike. These three-dimensional shapes offer a unique blend of complexity and elegance, challenging our understanding of geometry and pushing the boundaries of what we thought was possible.
But what secrets do these enigmatic structures hold? How can they be used to solve mathematical puzzles? In this section, we will dive deep into the world of galaxy polyhedra, exploring their connections to various puzzles and unraveling the secrets they hold.
Exploring the Connection

At first glance, it may seem puzzling why galaxy polyhedra are linked to mathematical puzzles. After all, these shapes are beautiful but seemingly abstract objects. However, upon closer inspection, their intricate geometry and symmetrical patterns reveal a hidden world of mathematical possibilities.
One of the key connections between galaxy polyhedra and mathematical puzzles lies in their ability to be disassembled and reassembled. Just like a puzzle, these shapes can be taken apart into their constituent pieces, revealing hidden relationships and interconnections.
The Puzzle Solving Power

When it comes to mathematical puzzles, galaxy polyhedra offer a unique challenge. Not only do they test our spatial reasoning skills, but they also require us to think outside the box and explore unconventional solutions.
The disassembly and reassembly of galaxy polyhedra can be thought of as a puzzle in itself. As we take apart the shape, we must carefully observe and understand the relationships between its components. This process of unraveling the structure can often lead to new insights and creative problem-solving approaches.
In conclusion, galaxy polyhedra are more than just beautiful objects. They hold the key to unlocking new dimensions of mathematical puzzles and challenging our thinking. By exploring the connections between these shapes and puzzles, we can unravel their secrets and broaden our understanding of mathematics. So, let’s embark on this fascinating journey and discover the hidden wonders of galaxy polyhedra.
Question-answer:
What are Galxe polyhedra?
Galxe polyhedra are a type of three-dimensional geometric shape that consists of regular polygons as their faces.
How many types of Galxe polyhedra are there?
There are six types of Galxe polyhedra: tetrahedron, octahedron, dodecahedron, icosahedron, cube, and cuboctahedron.
What are some mathematical puzzles related to Galxe polyhedra?
One mathematical puzzle related to Galxe polyhedra is trying to find the maximum number of non-overlapping cubes that can be packed inside a large cube. Another puzzle is trying to find the number of unique paths that can be taken in a cube from one vertex to another while only moving on the edges.
Is there any practical application of Galxe polyhedra?
Yes, Galxe polyhedra have practical applications in various fields such as architecture, chemistry, and computer graphics. For example, architects often use Galxe polyhedra as the basis for designing unique and aesthetically pleasing buildings.
What is the significance of studying the connection between Galxe polyhedra and mathematical puzzles?
The study of the connection between Galxe polyhedra and mathematical puzzles helps us gain a deeper understanding of the geometric properties of these shapes and enhances our problem-solving skills. It also provides insights into the mathematical principles that govern the behavior of these polyhedra.


