
Galxe polyhedra are a fascinating class of geometric shapes that offer endless possibilities for exploration. These three-dimensional structures are constructed using a combination of mathematical principles and artistic intuition, resulting in visually stunning and mathematically intriguing objects.
One of the defining features of galxe polyhedra is their intricate network of interconnected faces, edges, and vertices. Each face is carefully designed and positioned to create a harmonious balance between symmetry and complexity. The mathematical precision required to construct these shapes is truly remarkable, and it speaks to the deep connection between mathematics and art.
The representation of galxe polyhedra is an art form in and of itself. Artists and mathematicians alike are constantly exploring new ways to capture the essence of these shapes on paper and in digital media. Different techniques, such as shading, coloring, and perspective, are employed to enhance the beauty and depth of these geometric wonders.
Mathematicians have also developed various mathematical models and systems to describe and study galxe polyhedra. These models help us understand the underlying principles governing the formation and structure of these shapes. By analyzing the symmetries, angles, and proportions of galxe polyhedra, mathematicians can uncover hidden patterns and relationships that shed light on the nature of geometry and its role in the natural world.
The Mathematical Construction

The mathematical construction of galxe polyhedra involves several steps. First, we start with a set of vertices, which are the points in space that define the shape of the polyhedra. These vertices can be connected by edges, which are the line segments that form the sides of the polyhedra. The set of edges then create the faces of the polyhedra, which are the flat surfaces that enclose the space.
To construct a galxe polyhedra, we need to ensure that certain conditions are met. These conditions include the Euler’s formula, which states that the number of vertices, edges, and faces of a polyhedron must satisfy the equation: V – E + F = 2. This formula helps ensure that the polyhedra is a well-formed shape.
Once the vertices, edges, and faces of the polyhedra are defined, we can move on to the representation of the polyhedra. One common representation is the net, which is a 2D representation of the polyhedra that can be printed on a flat surface and folded to create the 3D shape. Another representation is the 3D model, which can be created using computer-aided design (CAD) software or 3D printing technology.
Mathematical construction is an important step in understanding and describing galxe polyhedra. It allows us to analyze their properties, study their symmetries, and explore their applications in various areas of science and engineering.
Definition and Basic Concepts
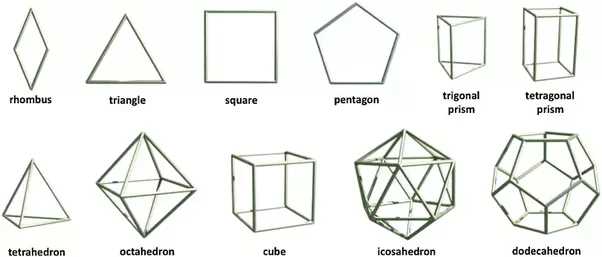
In mathematics, the construction and representation of Galaixe polyhedra involves the study of complex geometric objects known as polyhedra. A polyhedron is a three-dimensional solid or surface in space, composed of polygons. Each polygon, known as a face, is connected to neighboring faces by edges, and the edges come together at points called vertices.
Galaixe polyhedra, named after the mathematician Galaixe, are a special class of polyhedra that have distinctive properties. These polyhedra have all their faces and edges congruent and are perfectly symmetric. They possess a high degree of regularity and symmetry, making them fascinating objects of study in fields such as geometry, topology, and crystallography.
Polyhedral Elements
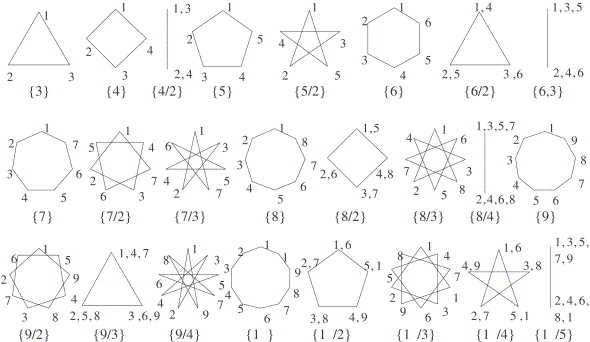
There are several key elements that define Galaixe polyhedra:
- Vertices: The points where the edges of the polyhedra intersect are called vertices.
- Edges: The line segments that connect the vertices are known as edges.
- Faces: The polygons that make up the surfaces of the polyhedra are called faces.
- Vertices Degrees: The number of edges that meet at each vertex is known as the vertex degree.
These elements work together to create the structure and characteristics of Galaixe polyhedra. The relationships between the vertices, edges, and faces determine the shape, symmetry, and regularity of the polyhedra.
Constructing and Representing Galaixe Polyhedra
There are various methods and approaches to construct and represent Galaixe polyhedra. One common technique is to start with a regular polyhedron, such as a Platonic solid, and perform operations such as truncation, augmentation, and stellation to create Galaixe polyhedra. These operations alter the original polyhedra by modifying the faces, edges, and vertices.
Representing Galaixe polyhedra can be done through various methods, such as physical models, computer-aided design, or mathematical formulas. The use of mathematical notation, matrices, and algorithms allows for precise and accurate representation of these complex geometric objects.
Applications
The study of Galaixe polyhedra has applications in various fields, including crystallography, architecture, physics, and art. Understanding their geometry and symmetry can provide insights into the arrangement of atoms in crystals, the design of architectural structures, the behavior of particles in physics, and the aesthetics of artistic creations.
| Field | Application |
|---|---|
| Crystallography | Analysis of crystal structures |
| Architecture | Design of structurally stable buildings |
| Physics | Understanding the behavior of particles in symmetry |
| Art | Creative inspiration and aesthetic design |
Overall, Galaixe polyhedra offer a rich and captivating area of study, providing a bridge between mathematics, science, and art.
Methods and Algorithms for Construction
In order to construct Galxe polyhedra, several methods and algorithms have been developed. These methods aim to efficiently and accurately create the intricate geometric structures of Galxe polyhedra.
Geometric Construction Methods

One of the most common methods for constructing Galxe polyhedra is through geometric construction. This method involves using simple geometric shapes, such as squares, triangles, and pentagons, as building blocks to construct the polyhedra.
For example, the truncated icosahedron, which is the most famous Galxe polyhedron, can be constructed by using 20 hexagons and 12 pentagons. Each pentagon is surrounded by five hexagons, creating a sphere-like shape.
Mathematical Algorithms
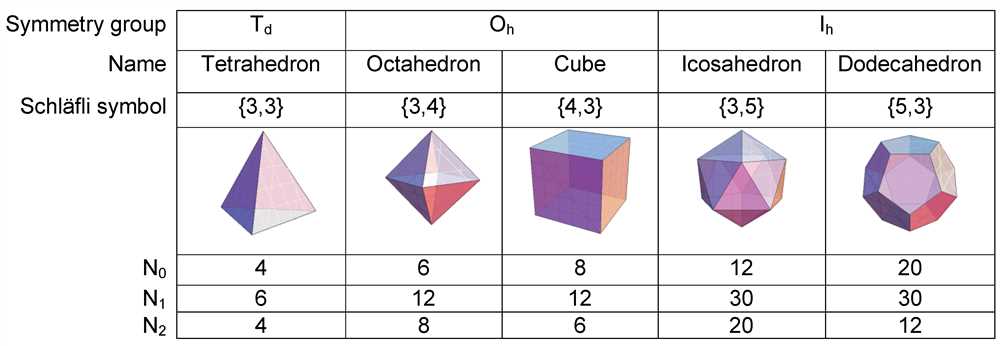
In addition to geometric construction methods, several mathematical algorithms have been developed for constructing Galxe polyhedra. These algorithms often involve complex mathematical calculations and formulas to determine the precise coordinates and dimensions of each vertex and face of the polyhedra.
One commonly used algorithm is the vertex-first algorithm, which starts by determining the coordinates of the vertices of the polyhedra. The algorithm then calculates the coordinates and dimensions of each face based on the positions of the vertices.
Computer-Aided Design (CAD)

With the advancement of computer technology, computer-aided design (CAD) software has become an invaluable tool for constructing Galxe polyhedra. CAD software allows for precise and efficient construction of the polyhedra, as well as the ability to visualize and manipulate the models in three-dimensional space.
Through CAD software, designers and mathematicians can input the necessary parameters and dimensions of the polyhedra, and the software will automatically generate the corresponding geometric structures. This greatly simplifies the construction process and allows for more complex and intricate Galxe polyhedra to be created.
Overall, the methods and algorithms for constructing Galxe polyhedra involve a combination of geometric construction, mathematical algorithms, and computer-aided design. These techniques enable the creation of complex and aesthetically pleasing polyhedra, contributing to the field of mathematics and geometry.
Representation of Galxe Polyhedra
Galxe polyhedra are geometric figures used to represent the quantum states of systems with a discrete symmetry, such as crystals and magnets. They are often used in solid-state physics to model and understand the behavior of materials and their electronic properties. These polyhedra are constructed using mathematical principles to accurately represent the symmetries and relationships of the underlying physical system.
Mathematical Construction

The mathematical construction of Galxe polyhedra involves the use of group theory and symmetry operations. Group theory is a branch of mathematics that studies the properties of groups, which are sets of elements and operations that satisfy certain axioms. In the context of Galxe polyhedra, group theory is used to characterize the symmetries and transformations of the system.
To construct a Galxe polyhedron, one starts with a high symmetry point group, which is a group of symmetries that leaves a point fixed in space. This point group is then used to generate a set of vectors, known as the basis vectors, which are used to construct the polyhedron. These basis vectors are chosen in such a way that they satisfy the symmetries of the point group.
Representation and Visualization
Once a Galxe polyhedron is constructed mathematically, it can be represented and visualized in various ways. One common representation is to use a 3D plot or diagram to show the shape and structure of the polyhedron. This can be done using computer graphics software or by hand-drawing.
Another way to represent Galxe polyhedra is through their connectivity or adjacency matrices. These matrices represent the relationships between the vertices or points of the polyhedron. By analyzing the connectivity matrix, one can gain insights into the topological properties of the polyhedron and its symmetries.
Additionally, Galxe polyhedra can be represented using symbolic expressions or mathematical equations that describe their geometric properties. These equations can be used to calculate various properties of the polyhedra, such as their volume, surface area, and symmetry elements.
- 3D plots or diagrams
- Connectivity or adjacency matrices
- Symbolic expressions or mathematical equations
In conclusion, Galxe polyhedra are mathematical representations of the symmetries and properties of systems with discrete symmetry. They are constructed using group theory and can be visualized in 3D plots, represented using connectivity matrices, or described using symbolic expressions. These representations help scientists understand and analyze the behavior of materials and their electronic properties.
Abstract Representation and Projections
Abstract representation and projections are essential tools in the mathematical construction and analysis of galxe polyhedra. They allow us to visually understand and manipulate complex geometrical structures, enabling us to explore their properties and relationships.
In the context of galxe polyhedra, an abstract representation refers to a simplified, two-dimensional depiction of the polyhedra that captures its essential features and relationships. This representation can be created using various techniques, such as projection, unfolding, or graph representation.
Projections, on the other hand, involve the transformation of the polyhedra onto a lower-dimensional plane. This allows for a more manageable and understandable representation of the polyhedra’s structure. Projections can be created using different methods, including the use of parallel or central projection techniques.
The choice of projection method depends on the specific goals and requirements of the analysis. For example, parallel projection is often used when preserving lengths and angles is important, while central projection is commonly employed when creating perspective views.
In addition to abstract representation and projections, other mathematical tools, such as graph theory and combinatorial optimization, are often used to analyze galxe polyhedra. These tools help in understanding the connectivity and symmetry of the polyhedral structures, as well as their combinatorial properties.
Overall, abstract representation and projections play a crucial role in the mathematical study of galxe polyhedra. They help in simplifying complex geometries and visualizing their structures, enabling researchers to explore and understand their properties in a more accessible manner.
Computer-aided Modeling and Visualization

Computer-aided modeling and visualization play a significant role in the mathematical construction and representation of Galxe polyhedra. These tools allow mathematicians and researchers to create, manipulate, and explore complex geometric structures in a virtual environment.
With computer-aided modeling software, such as CAD programs or 3D modeling software, mathematicians can create and define the precise mathematical equations and algorithms that describe the geometry of Galxe polyhedra. This allows for the generation of accurate and detailed models that would be difficult, if not impossible, to construct by hand.
In addition to creating the models, computer-aided visualization tools enable mathematicians to visualize and interact with the constructed polyhedra. Through the use of rendering techniques, these tools can generate realistic and visually appealing representations of the polyhedra, allowing for a better understanding and analysis of their properties.
Benefits of Computer-aided Modeling and Visualization
Computer-aided modeling and visualization offer several benefits in the study of Galxe polyhedra:
- Precision and accuracy: Computer-aided modeling allows for precise mathematical definitions of Galxe polyhedra, ensuring accurate representations and calculations.
- Efficiency: Creating and manipulating Galxe polyhedra using computer-aided tools is faster and more efficient than manual construction methods.
- Exploration and experimentation: Visualization tools enable mathematicians to explore different configurations and variations of Galxe polyhedra, leading to new insights and discoveries.
- Communication and collaboration: Computer-aided models and visualizations can be easily shared and discussed among mathematicians, facilitating collaboration and knowledge exchange.
Challenges and Limitations
Despite the benefits, computer-aided modeling and visualization also face certain challenges and limitations:
- Complexity: Galxe polyhedra can have intricate geometries and properties, making their accurate representation and visualization computationally challenging.
- Algorithmic limitations: Finding efficient algorithms to construct and manipulate Galxe polyhedra remains an active research area, as some properties and operations are still not well-defined.
- Hardware requirements: In order to handle the computational demands of complex Galxe polyhedra, powerful hardware and computing resources are often necessary.
- Data interpretation: Interpreting and analyzing the visualized results can be a complex task, requiring mathematical expertise and careful consideration of the limitations of the modeling and visualization techniques used.
In conclusion, computer-aided modeling and visualization are valuable tools in the study of Galxe polyhedra. They enable mathematicians to create accurate models, explore different configurations, and communicate their findings more effectively. However, challenges and limitations exist, emphasizing the need for further research and advancements in this field.
Question-answer:
What is the mathematical construction of Galxe Polyhedra?
The mathematical construction of Galxe Polyhedra involves connecting the midpoints of the edges of a polyhedron to form a new set of faces.
How are Galxe Polyhedra represented mathematically?
Galxe Polyhedra can be represented mathematically using edge connections, face connections, and vertex coordinates.


