Galaxy polyhedra are a fascinating area of study in the field of mathematics. These intricate shapes, which resemble celestial bodies, have captured the imagination of both mathematicians and astronomers alike. The study of galaxy polyhedra involves the exploration of complex mathematical algorithms and geometric principles, as well as the application of these ideas to the real world.
Mathematical algorithms play a crucial role in understanding the intricate formations of galaxy polyhedra. These algorithms, which are a set of rules or processes, help mathematicians explore the relationships between the vertices, edges, and faces of these polyhedra. Through the implementation of algorithmic procedures, mathematicians are able to unravel the mysteries behind the formation and properties of these fascinating shapes.
One fundamental algorithm used in the study of galaxy polyhedra is the convex hull algorithm. This algorithm allows mathematicians to determine the smallest convex shape that completely encloses a given set of points in space. By applying this algorithm to the points representing the vertices of a galaxy polyhedron, mathematicians are able to determine its overall shape and structure. The convex hull algorithm provides crucial insights into the formation and development of these intriguing polyhedra.
Understanding the Basics
To understand the mathematical algorithms behind Galxe polyhedra, it is essential to have a basic understanding of polyhedra and their properties. A polyhedron is a three-dimensional geometric shape with flat faces, straight edges, and sharp vertices. Each face of a polyhedron is a polygon, which can be a triangle, quadrilateral, pentagon, or any other regular or irregular polygon.
Polyhedron Elements
The main elements of a polyhedron include:
- Vertices: These are the points where the edges of a polyhedron meet. The plural form of vertex is vertices.
- Edges: These are the line segments where two vertices of a polyhedron meet. They form the boundaries of the faces.
- Faces: These are the flat surfaces of a polyhedron. Each face is a polygon.
- Edges: These are the line segments where two vertices of a polyhedron meet. They form the boundaries of the faces.
- Vertices: These are the points where the edges of a polyhedron meet. The plural form of vertex is vertices.
These elements work together to give a polyhedron its shape and structure. Polyhedra can be classified based on the number of faces they have, such as tetrahedra (4 faces), octahedra (8 faces), and dodecahedra (12 faces).
Euler’s Formula

Euler’s formula, named after the Swiss mathematician Leonhard Euler, relates the number of vertices, edges, and faces of a polyhedron. It states:
V + F – E = 2
Where V represents the number of vertices, F represents the number of faces, and E represents the number of edges. This formula holds true for all polyhedra, whether they are regular or irregular.
Understanding these basic concepts of polyhedra and Euler’s formula is crucial in comprehending the mathematical algorithms used to generate and analyze Galxe polyhedra.
| Polyhedron Name | Number of Faces |
|---|---|
| Tetrahedron | 4 |
| Hexahedron (Cube) | 6 |
| Octahedron | 8 |
| Dodecahedron | 12 |
| Icosahedron | 20 |
The Beauty of Mathematical Symmetry
Mathematical symmetry is a mesmerizing concept that permeates many areas of mathematics and the natural world. Symmetry can be found in art, architecture, and even in the arrangement of celestial bodies. It is the harmony and balance created by repetition and reflection that gives rise to the beauty of symmetry.
One of the fascinating aspects of symmetry is that it can be described and analyzed using mathematical algorithms. These algorithms allow us to understand the patterns and relationships that underlie symmetric forms.
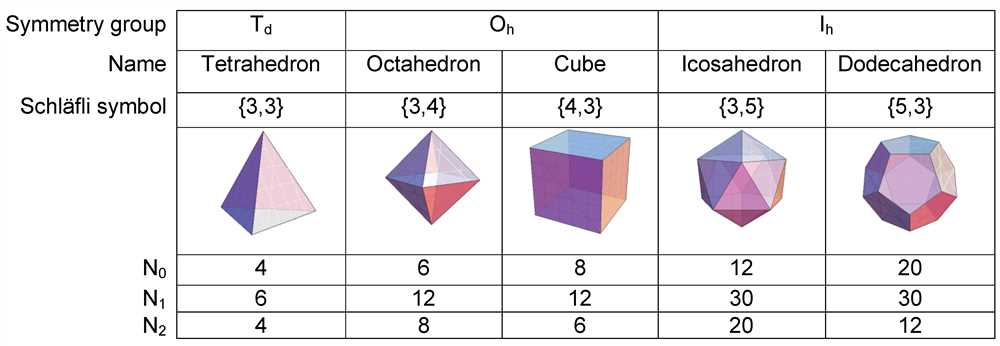
One of the most famous examples of mathematical symmetry is the study of polyhedra. Polyhedra are three-dimensional shapes with flat faces and straight edges. The various types of polyhedra exhibit different degrees and types of symmetry.
For instance, the Platonic solids, which include the cube and the tetrahedron, are highly symmetrical. Each face of a Platonic solid is the same regular polygon, and the arrangement of the faces and vertices maintain the same symmetrical pattern.
Another example of mathematical symmetry can be seen in the study of fractals. Fractals are infinitely complex patterns that repeat themselves at different scales. The mathematical algorithms used to generate fractals, such as the Mandelbrot set, reveal intricate symmetrical patterns that are awe-inspiring.
In addition to their aesthetic appeal, mathematical symmetry has practical applications. It is used in fields such as computer graphics, data compression, cryptography, and even physics. The symmetrical patterns and structures found in nature have inspired engineers and scientists to develop innovative solutions and technologies.
The beauty of mathematical symmetry lies in its ability to reveal hidden patterns and structures in the world around us. It allows us to appreciate the elegance and harmony in nature and to understand the underlying principles that govern the universe. Through the study of mathematical algorithms, we can explore and unlock the secrets of symmetry, adding depth and meaning to our understanding of the world.
| Examples of Symmetry |
|---|
| Snowflakes |
| Butterflies |
| Flowers |
Exploring Regular Polyhedral Models
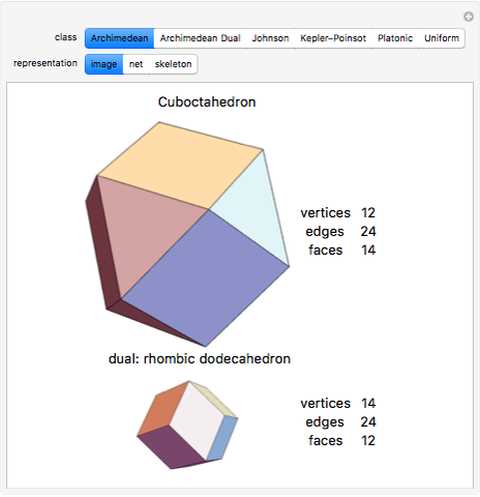
Regular polyhedra are fascinating mathematical objects that have been studied for centuries. They are three-dimensional solids composed of identical polygonal faces, where each vertex is the meeting point of the same number of edges. These polyhedra have a high degree of symmetry and can be found in various fields such as crystallography, architecture, and game design.
One way to explore regular polyhedral models is through their face, vertex, and edge configurations. For example, the Platonic solids are a set of five regular polyhedra that are highly symmetric: the tetrahedron with 4 equilateral triangular faces, the cube with 6 square faces, the octahedron with 8 equilateral triangular faces, the dodecahedron with 12 regular pentagonal faces, and the icosahedron with 20 equilateral triangular faces.
These regular polyhedra have unique characteristics that make them interesting to study. For instance, the Platonic solids have the property of having the same number of faces meeting at each vertex. This property is known as the vertex-transitive property, and it contributes to their symmetric nature.
Another way to explore regular polyhedral models is through their dual polyhedra. The dual polyhedron is formed by swapping the faces and vertices of the original polyhedron. This can lead to surprising results, such as the fact that the dual of the cube is the octahedron, and vice versa. Studying the dual polyhedra can reveal hidden symmetries and relationships between different regular polyhedra.
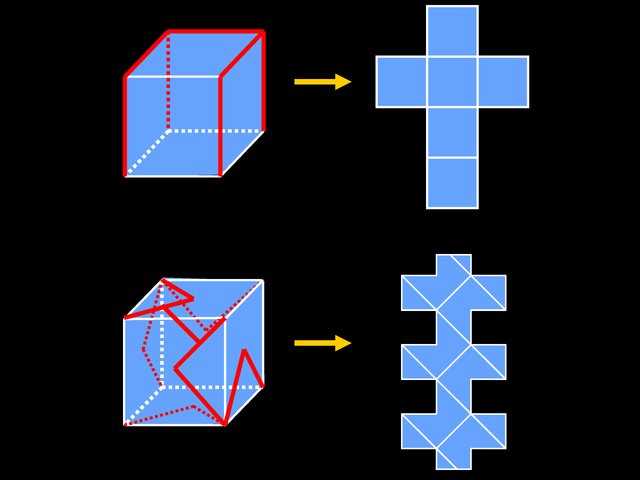
Regular polyhedra can also be explored through their net representations. A net is a 2D representation of a 3D object that can be cut and folded to form the original polyhedron. By analyzing the nets of regular polyhedra, one can gain insights into their structural properties, such as the arrangement of faces and vertices.
In conclusion, exploring regular polyhedral models offers a deeper understanding of their mathematical properties and aesthetic qualities. Whether through their face, vertex, and edge configurations, their dual polyhedra, or their net representations, these polyhedra continue to captivate mathematicians, scientists, and artists alike.
Mathematical Algorithms in Action
The study of mathematical algorithms has a wide range of applications and one area where their effectiveness is clearly demonstrated is in the creation and manipulation of Galxe polyhedra.
One key algorithm used in the construction of Galxe polyhedra is the iterative subdivision algorithm. This algorithm starts with a simple initial shape, such as a cube or an icosahedron, and then repeatedly subdivides each face into smaller triangles. The process is repeated for a specified number of iterations, resulting in a more complex polyhedron with a higher level of detail.
Another algorithm involved in the creation of Galxe polyhedra is the edge flipping algorithm. This algorithm aims to improve the connectivity and shape of the polyhedron by iteratively flipping edges based on certain criteria. By selectively flipping edges, the algorithm can create more uniform and aesthetically pleasing shapes.
Additionally, the optimization algorithm is used in the generation of Galxe polyhedra. This algorithm aims to find the optimal placement and orientation of the polyhedron’s vertices and edges to minimize certain properties, such as surface area or distortion. By iteratively adjusting the positions of the vertices and edges, the algorithm can optimize the overall shape of the polyhedron.
Furthermore, the projection algorithm is crucial in the visualization and rendering of Galxe polyhedra. This algorithm maps the vertices of the polyhedron onto a 2D plane, taking into account perspective and depth. By using this algorithm, a 2D representation of the polyhedron can be created, allowing for easier analysis and interpretation.
In conclusion, mathematical algorithms play a fundamental role in the creation and manipulation of Galxe polyhedra. Through algorithms such as iterative subdivision, edge flipping, optimization, and projection, these intricate and aesthetically pleasing shapes can be effectively generated and visualized. The application of mathematical algorithms in this context highlights their power and versatility in the field of geometry and visualization.
Computing Polyhedra using Geometric Transformations
In order to generate and manipulate polyhedra, mathematical algorithms rely on a variety of geometric transformations. These transformations allow for the creation of complex three-dimensional shapes from simpler components, and the manipulation of these shapes to perform various operations.
Translation
Translation is one of the fundamental geometric transformations used in computing polyhedra. It involves moving points, lines, or entire objects from one location to another without changing their size, shape, or orientation. In the context of polyhedra, translation can be used to shift the position of vertices, edges, and faces to create new shapes or transform existing ones.
Rotation
Rotation is another key transformation used in computing polyhedra. It involves rotating objects around a fixed point or axis. In the context of polyhedra, rotation can be used to change the orientation of vertices, edges, and faces. By applying different rotation angles and axes, complex transformations can be achieved, leading to the creation of intricate polyhedral structures.
These geometric transformations can be combined and applied in sequence to generate a wide range of polyhedral shapes. For example, translating a set of vertices to form a basic shape, followed by a series of rotations, can result in the creation of complex polyhedra with unique characteristics.
In addition to generating polyhedra, geometric transformations are also useful for performing operations such as scaling, shearing, and reflection. These operations can further manipulate polyhedral shapes and enable the creation of symmetrical structures or patterns.
| Geometric Transformation | Description |
|---|---|
| Translation | Moves points, lines, or objects to a new location |
| Rotation | Rotates objects around a fixed point or axis |
| Scaling | Changes the size of objects by stretching or compressing them |
| Shearing | Skews objects along a specific axis |
| Reflection | Creates a mirror image of objects |
By utilizing these geometric transformations, mathematical algorithms can effectively compute and manipulate polyhedra, enabling researchers and designers to explore and create complex three-dimensional structures.
Real-World Applications
The mathematical algorithms used to construct and analyze Galxe polyhedra have numerous real-world applications. Here are a few examples:
Architectural Design
Galxe polyhedra provide unique and aesthetically pleasing shapes that can be used in architectural design. Their complex geometries can be incorporated into building facades, interior spaces, and structural elements to create visually stunning and structurally sound designs.
Molecular Modeling
The study of molecular structures is crucial in fields such as chemistry and biology. Galxe polyhedra can be used to model the three-dimensional arrangement of atoms within molecules, providing insights into molecular properties and interactions. These models help scientists understand how different compounds behave and can guide the design of new drugs and materials.
| Field | Application |
|---|---|
| Computer Graphics | Galxe polyhedra can be used to generate visually appealing shapes and animations in computer graphics and virtual reality applications. |
| Robotics | The algorithms behind Galxe polyhedra can be used to plan and control the movements of robotic limbs and manipulators, enabling precise and efficient operations. |
| Network Optimization | Galxe polyhedra can be used to model and optimize the flow of resources in networks, such as transportation networks or computer networks, to minimize costs and improve efficiency. |
These are just a few examples of how the mathematical algorithms behind Galxe polyhedra have practical applications in various fields. The beauty and complexity of these structures make them a fascinating area of study for mathematicians, engineers, and scientists alike.
Galxe Polyhedra in Architecture and Design
Galxe polyhedra have gained significant attention in the field of architecture and design due to their unique geometric properties and fascinating aesthetic appeal. These polyhedra, which are derived from the underlying mathematical algorithms, have become popular elements in various architectural and design projects.
The Beauty of Galxe Polyhedra
The intricate and symmetrical patterns created by galxe polyhedra offer a visually captivating experience. The mesmerizing shapes and interlocking polygons create a sense of harmony and balance in architectural structures and design objects.
Designers and architects often incorporate galxe polyhedra into their projects to introduce a contemporary and artistic touch. The complexity and precision of these geometric shapes can add an element of sophistication and elegance to any design.
Practical Applications

Galxe polyhedra not only serve as decorative elements but also offer practical applications. The symmetrical nature of these geometric forms makes them ideal for structural purposes.
Architects leverage the strength and stability of galxe polyhedra to create structurally sound buildings and bridges. The interlocking polygons distribute the weight evenly, providing support and enhancing the durability of the structures.
Moreover, galxe polyhedra can also be translated into functional design objects such as lighting fixtures and furniture. The unique shapes and patterns add a creative flair to these objects, making them stand out as artistic pieces.
In conclusion, galxe polyhedra play a pivotal role in both the architectural and design world. Their captivating aesthetic appeal and practical applications make them a popular choice among designers and architects seeking to create visually stunning and structurally sound works.
Question-answer:
What are Galxe polyhedra?
Galxe polyhedra are a type of 3D geometric shape that are composed of interconnected cells. Each cell of a Galxe polyhedron is a regular polyhedron.
What are some examples of Galxe polyhedra?
Some examples of Galxe polyhedra include the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. These are all regular polyhedra.


