The world of mathematics is filled with fascinating concepts and structures that often go unnoticed in our everyday lives. One such concept is the study of polyhedra, which are three-dimensional shapes with flat polygonal faces. These shapes can be found in various fields of science and art, and their intricate patterns and sequences have captured the attention of mathematicians for centuries.
Galxe polyhedra are a specific class of polyhedra that exhibit unique mathematical properties. Named after mathematician Carl Galxe, these polyhedra are characterized by their symmetrical arrangements of faces and vertices. Each vertex of a Galxe polyhedron connects to a set number of faces, creating a harmonious relationship between the different elements of the shape.
One of the most fascinating aspects of Galxe polyhedra is the mathematical sequences that can be derived from their structures. By examining the number of vertices, edges, and faces of different Galxe polyhedra, mathematicians have discovered a series of patterns and formulas that govern their properties. These sequences, known as Galxe sequences, provide insights into the underlying mathematical principles that govern the formation of these shapes.
Exploring the mathematical patterns and sequences of Galxe polyhedra not only deepens our understanding of geometry and topology, but also has practical applications in various fields such as computer graphics, architecture, and biology. By studying the relationships between the different elements of these shapes, mathematicians can create new algorithms for modeling and rendering three-dimensional objects, design innovative architectural structures, and even gain insights into the organization of biological systems.
Understanding the Mathematical Structure of Galxe Polyhedra
Galxe polyhedra are a fascinating class of mathematical objects that have a unique geometric structure. These polyhedra are made up of regular polygons, such as triangles, squares, and pentagons, that meet at the same number of edges and vertices. While they may seem complex at first, understanding the mathematical structure of Galxe polyhedra can provide insights into their symmetry and properties.
Symmetry in Galxe Polyhedra

One of the key features of Galxe polyhedra is their symmetry. These polyhedra exhibit various types of symmetry, including rotational, reflectional, and translational symmetry. Rotational symmetry is when a figure can be rotated around a central point and still look the same. Reflectional symmetry is when a figure can be reflected across a line and still maintain its shape. Translational symmetry is when a figure can be moved in a certain direction without changing its shape. These types of symmetry in Galxe polyhedra are a result of their regular polygonal faces and the arrangement of these faces in space.
Properties of Galxe Polyhedra
Galxe polyhedra have several interesting properties that make them unique in the realm of geometry. First, they have a constant vertex connectivity, which means that each vertex of the polyhedra is connected to the same number of edges. This gives Galxe polyhedra a sense of balance and uniformity. Second, Galxe polyhedra have a constant edge length, meaning that all edges of the polyhedra are of equal length. Finally, they have a constant face angle, which refers to the angle between adjacent faces. This face angle is dependent on the type of regular polygon that makes up the faces of the polyhedra.
The mathematical structure of Galxe polyhedra is intricate and fascinating. By studying their symmetry and properties, mathematicians and researchers can gain a deeper understanding of these unique geometric objects. Through this understanding, new insights and applications can be discovered, further advancing our knowledge of mathematics and its applications in various fields.
Exploring Mathematical Patterns in Galxe Polyhedra
The study of galxe polyhedra involves the exploration of mathematical patterns and sequences that arise from these unique three-dimensional shapes. Galxe polyhedra are a special class of polyhedra that have symmetrical structures and exhibit fascinating geometric properties.
One of the key mathematical patterns observed in galxe polyhedra is the presence of vertex-transitive arrangements, where each vertex has an identical configuration of edges and faces. This property allows for the creation of beautiful and symmetrical structures that can be seen in various natural and man-made forms.
Furthermore, galxe polyhedra often exhibit self-similarity, where smaller copies of the overall shape can be found within the larger structure. This fractal-like property can be seen in the intricate patterns and complex geometries of galxe polyhedra, giving them an aesthetic appeal and making them a fascinating subject of study for mathematicians and artists alike.
In addition to their visual appeal, galxe polyhedra also have practical applications in various fields. For example, their symmetrical arrangements and robust structures make them suitable for architectural designs, allowing for efficient use of materials and structural stability.
The exploration of mathematical patterns in galxe polyhedra also extends to the study of their sequences. By examining the relationships between the edge lengths, face angles, and vertex configurations of different galxe polyhedra, mathematicians can uncover interesting sequences and properties that contribute to our understanding of geometry and shape formation.
In conclusion, exploring the mathematical patterns in galxe polyhedra offers a gateway to understanding the intricate relationships between geometry and structure. From their symmetrical arrangements to their self-similarity and practical applications, galxe polyhedra provide a rich landscape for mathematical exploration and discovery.
Sequences and Properties of Galxe Polyhedra
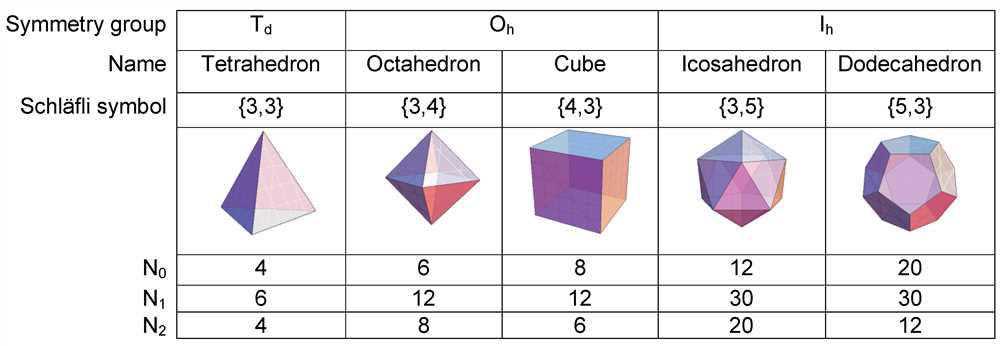
In the study of Galxe polyhedra, various mathematical patterns and sequences emerge that allow for a deeper understanding of their properties and structural characteristics. By exploring these sequences, researchers have been able to uncover unique features of Galxe polyhedra and identify their distinct attributes.
Fibonacci Sequence

One of the most notable sequences found in Galxe polyhedra is the Fibonacci sequence. This sequence, named after the Italian mathematician Leonardo of Pisa, is a series of numbers where each number is the sum of the two preceding ones. It starts with 0 and 1, and the pattern continues indefinitely.
Researchers have discovered that certain Galxe polyhedra exhibit Fibonacci-like patterns in their structure. The number of vertices, edges, and faces of these polyhedra often follow ratios that resemble the Fibonacci sequence. This discovery has led to further investigations into the underlying mathematics of Galxe polyhedra.
Geometric Progressions
Another sequence that appears in the properties of Galxe polyhedra is the geometric progression. Geometric progressions are sequences in which each term is obtained by multiplying the preceding term by a constant ratio.
In the case of Galxe polyhedra, the geometric progression can be observed in the increase in the number of vertices, edges, and faces as the complexity of the polyhedron increases. Each new polyhedron in the sequence has a higher number of vertices, edges, and faces compared to the previous one, following a consistent ratio.
This geometric progression allows researchers to predict the properties of Galxe polyhedra based on the properties of simpler polyhedra. It provides a systematic approach to understanding the structural characteristics of these complex shapes.
Euler’s Formula

Euler’s formula is another significant property that applies to Galxe polyhedra. The formula states that for any given polyhedron, the number of vertices (V), edges (E), and faces (F) are related by the equation V – E + F = 2.
This formula holds true for Galxe polyhedra as well, contributing to their overall mathematical consistency. By manipulating the equation, researchers can derive various properties and relationships between the vertices, edges, and faces of Galxe polyhedra.
- The Fibonacci sequence is often present in the number of vertices, edges, and faces of Galxe polyhedra.
- Geometric progressions describe the increase in these properties as the complexity of the polyhedra increases.
- Euler’s formula establishes a fundamental relationship between the vertices, edges, and faces of Galxe polyhedra.
By studying these sequences and properties, researchers can gain insights into the underlying mathematical principles of Galxe polyhedra and further explore their unique characteristics.
Question-answer:
What are galaxy polyhedra?
Galaxy polyhedra are geometric shapes that have a star-like pattern. They are three-dimensional structures consisting of interconnected triangular or polygonal faces.
How are galaxy polyhedra different from regular polyhedra?
Unlike regular polyhedra, galaxy polyhedra have a more complex and intricate structure. They exhibit a star-like pattern with edges that extend outward from a central vertex.
What are some mathematical patterns and sequences found in galaxy polyhedra?
One mathematical pattern found in galaxy polyhedra is the golden ratio, which can be seen in the proportions of the faces and edges. Another pattern is the Fibonacci sequence, which appears in the number of faces, edges, and vertices.
How can the mathematical patterns and sequences in galaxy polyhedra be used?
The mathematical patterns and sequences in galaxy polyhedra can be used to study and understand the underlying mathematical principles that govern their formation. They can also be used in various applications such as architecture, design, and computer graphics.
Can galaxy polyhedra be found in nature?
Yes, galaxy polyhedra can be found in nature. Some examples include certain crystals, virus structures, and molecular arrangements. Nature often utilizes these geometric patterns for their structural stability and efficiency.


