
When one thinks of symmetry, the mind often drifts to the natural world – the spiraling patterns of a sunflower, the perfect concentric circles of a peacock’s feathers. But what if we told you that there is a whole world of symmetry that exists beyond the realm of nature? Enter the captivating world of Galxe polyhedra – geometric forms that are not only mathematically fascinating but also possess a unique aesthetic appeal.
Galxe polyhedra, also known as Goldberg polyhedra, are a special subset of polyhedra with a profound aesthetic impact. These three-dimensional structures embody a mesmerizing balance between symmetry and complexity, with their meticulously arranged vertices, edges, and faces. Their intricate patterns and symmetrical arrangements are a testament to the harmony and beauty that can be found in mathematical concepts.
The symmetrical precision of Galxe polyhedra is not only awe-inspiring but also serves a practical purpose. These polyhedra find applications in a wide range of fields, including architecture, chemistry, and even virtual reality design. Their symmetrical nature makes them perfect candidates for the design of complex molecular structures, architectural frameworks, and digital graphics that require an optimal distribution of points and angles.
The Beauty of Galxe Polyhedra
Galxe polyhedra are a fascinating subject in mathematics and geometry due to their intricate symmetry and awe-inspiring aesthetics. These unique three-dimensional structures are formed by combining regular polygons in a specific pattern, creating a mesmerizing display of shapes and angles.
Intricate Symmetry
One of the most remarkable aspects of Galxe polyhedra is their intricate symmetry. Each face, edge, and vertex is precisely positioned to create a harmonious balance within the structure. The symmetries in Galxe polyhedra are often based on rotational or reflectional symmetries, resulting in a visually striking object.
Aesthetics and Visual Appeal
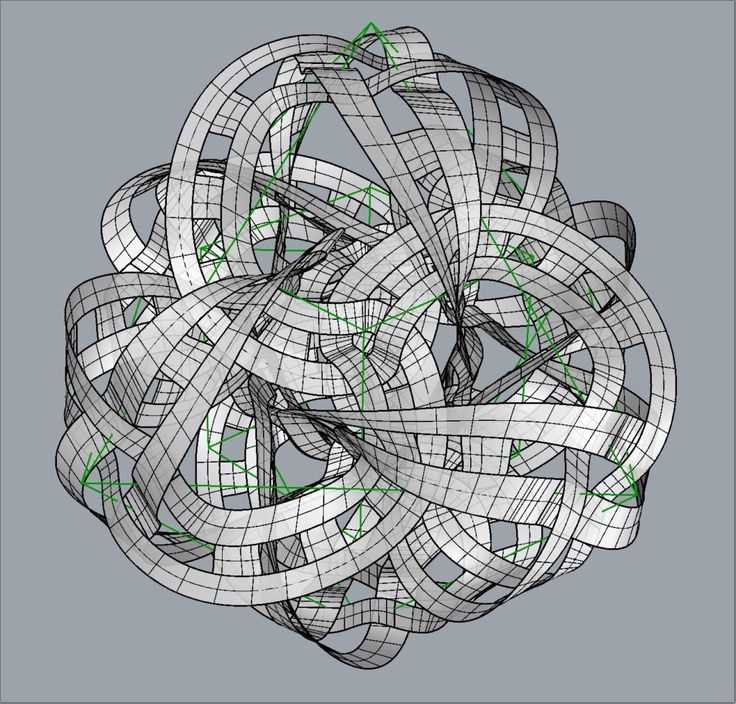
The aesthetics of Galxe polyhedra are truly captivating. The perfect symmetry and precise arrangement of shapes evoke a sense of beauty and elegance. The interplay of different polygons and angles creates an intricate web of lines and curves, which is visually pleasing and intriguing.
Furthermore, the regularity of the polygons used in Galxe polyhedra adds to their visual appeal. Regular polygons, such as equilateral triangles, squares, and pentagons, possess a natural symmetry that enhances the overall aesthetic of the polyhedra. The combination of these regular polygons in various configurations further adds to the beauty and complexity of Galxe polyhedra.
Overall, the beauty of Galxe polyhedra lies in their intricate symmetry and captivating aesthetics. These structures continue to inspire mathematicians, artists, and enthusiasts alike, showcasing the elegance and wonder of mathematics in the physical world.
Exploring the Mathematical Structure

The intricate symmetry and aesthetic appeal of Galxe Polyhedra are not just visually stunning, but are also deeply rooted in mathematics. These fascinating geometric figures are built upon complex mathematical principles, making them a subject of great interest for mathematicians, scientists, and artists alike.
At the core of Galxe polyhedra lies the concept of symmetry. Symmetry is a fundamental property of nature that can be found in many forms, from the elegance of a snowflake to the beauty of a flower petal. Galxe polyhedra take this concept of symmetry to a whole new level, showcasing a mesmerizing array of symmetrical patterns and shapes.
Mathematically, Galxe polyhedra are composed of a network of vertices, edges, and faces, forming a three-dimensional structure. The vertices represent points in space, the edges represent the connections between these points, and the faces represent the flat surfaces that enclose the space.
One of the key mathematical properties of Galxe polyhedra is their ability to tessellate space. Tessellation refers to the process of covering a surface or space with a pattern of geometric shapes, without any gaps or overlaps. Galxe polyhedra are especially intriguing in this regard, as they can tessellate space in a way that creates a visually pleasing and harmonious arrangement of shapes.
A rich history and cultural significance
The exploration of Galxe polyhedra and their mathematical structure has a rich history that spans across different cultures and time periods. Ancient civilizations such as the Egyptians, Greeks, and Chinese were aware of these geometric forms and incorporated them into their artwork, architecture, and religious symbolism.
Today, Galxe polyhedra continue to captivate the imagination of mathematicians and artists, who see in them not only aesthetic beauty but also a representation of profound mathematical concepts. The study of Galxe polyhedra has led to breakthroughs in fields such as crystallography, materials science, and computer graphics.
Unveiling the secrets of Galxe polyhedra

Exploring the mathematical structure of Galxe polyhedra involves delving into a realm where symmetry, geometry, and mathematics intertwine. Through the use of advanced mathematical techniques and computer modeling, researchers are able to uncover the intricate details and properties of these mesmerizing figures.
From uncovering new symmetries to understanding the impact of these structures on physical phenomena, the study of Galxe polyhedra opens up a world of possibilities for mathematical exploration. By pushing the boundaries of our knowledge, we can gain a deeper understanding of the fundamental principles that govern our universe.
The Role of Galxe Polyhedra in Design and Architecture
Galxe polyhedra, with their intricate symmetry and aesthetics, have been increasingly recognized for their potential impact in design and architecture. These unique three-dimensional structures offer a variety of applications in various fields, ranging from art installations to building facades.
Inspiration for Design
The complex arrangement of polygons in galxe polyhedra serves as a source of inspiration for designers seeking to create visually engaging and innovative products. The symmetrical patterns and aesthetic qualities of galxe polyhedra can be translated into various design elements, such as furniture, lighting fixtures, and decorative objects. By incorporating these geometric principles into their creations, designers can infuse a sense of elegance and harmony into their designs.
Architectural Applications
Galxe polyhedra also have significant potential in architectural applications. The intricate symmetry and geometrical precision of these structures can be used to create visually striking building facades, transforming mundane structures into works of art. The unique shapes and patterns of galxe polyhedra can provide a captivating visual experience for inhabitants and passersby, enhancing the overall aesthetics of the built environment.
Additionally, galxe polyhedra can be utilized as structural components, offering strength and stability to architectural designs. The inherent stability of these structures makes them suitable for constructing lightweight and strong structures, such as pavilions or temporary shelters. By integrating galxe polyhedra into architectural designs, architects can explore new possibilities in the construction industry, pushing the boundaries of what is achievable.
In conclusion, galxe polyhedra play a vital role in design and architecture due to their intricate symmetry and aesthetics. As a source of inspiration for designers and architects, these unique structures offer endless possibilities for creating visually captivating and innovative products. Whether used as design elements or as architectural components, galxe polyhedra have the potential to enhance the visual appeal and functionality of various design and architectural projects.
Applications in Science and Technology
The study of Galxe polyhedra has numerous applications in various scientific and technological fields. These unique geometric shapes have been found to possess a number of fascinating properties that make them useful in a wide range of applications.
Crystallography
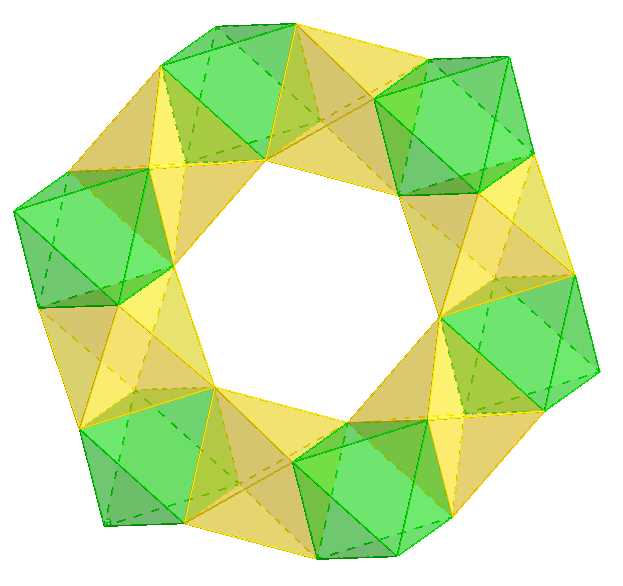
Galxe polyhedra have played a significant role in the field of crystallography. The precise symmetry and aesthetics of these polyhedra have helped researchers understand the atomic arrangement and structure of crystals. By studying the internal symmetry of Galxe polyhedra, scientists can gain valuable insights into the nature and behavior of different types of crystals.
The symmetrical arrangement of atoms within a crystal lattice can be accurately represented by Galxe polyhedra models. These models allow scientists to visualize and analyze the crystal structure, making it easier to study crystal properties such as symmetry, lattice spacing, and crystal habit.
Nanotechnology
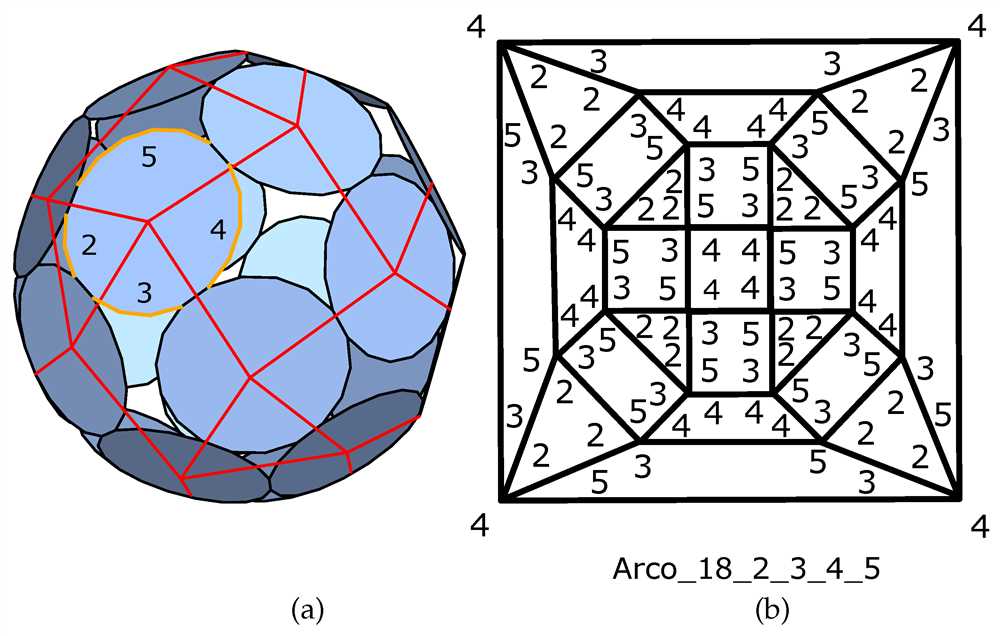
Galxe polyhedra are also being explored for their potential applications in nanotechnology. The intricate symmetry and aesthetics of these geometric shapes make them ideal candidates for constructing nanoscale structures with precise control over shape and size.
By using Galxe polyhedra as building blocks, researchers can create complex nanostructures with unique properties and functionalities. These structures have the potential to revolutionize various fields, such as electronics, medicine, and energy.
| Field | Potential Applications |
|---|---|
| Electronics | Development of high-performance microchips and nanoscale electronic devices. |
| Medicine | Design of targeted drug delivery systems and advanced biomaterials. |
| Energy | Creation of efficient solar cells and energy storage devices. |
By harnessing the unique properties of Galxe polyhedra, scientists and engineers are pushing the boundaries of nanotechnology and unlocking new possibilities for the future.
Question-answer:
What are galxe polyhedra?
Galxe polyhedra are a type of three-dimensional geometric object that have intricate symmetry and aesthetics. They are formed by connecting multiple regular polygons to create a solid shape.
Can you give some examples of galxe polyhedra?
Some examples of galxe polyhedra include the tetrahedron, hexahedron, octahedron, dodecahedron, and icosahedron. These are all regular polyhedra that have symmetrical faces and vertices.
What is the significance of the symmetry and aesthetics of galxe polyhedra?
The symmetry and aesthetics of galxe polyhedra make them aesthetically pleasing and visually interesting. The intricate patterns and shapes created by the regular polygons can be found in art, architecture, and nature, and they have been studied and admired by mathematicians and artists for centuries.


